|
sonidos de la justa entonación / Sistemas de entonación históricos
Sistemas de entonación históricosHaz clic aquí para escuchar el archivo sonoro: archivo mp3 (2.329 KB) Se recomienda escuchar el archivo sonoro con auriculares a volumen moderado. (Si trabajas con Chrome y se abre el archivo en la misma ventana del navegador, haz clic con el botón derecho y pulsa "Abrir enlace en una ventana nueva"; después puedes reducir su tamaño con el botón usual del cuadradito del extremo superior derecho a fin de poder leer al mismo tiempo el indicador de tiempo y el contenido en esta misma página.) Además de los sistemas temperado, pitagórico y justo, veremos también en este archivo otros sistemas históricos, como el temperamento mesotónico y algunos de los "buenos temperamentos" barrocos. Para ello, escucharemos dos cadencias perfectas, una mayor y otra menor (esta última, con el acorde final mayor), en cada uno de los sistemas: 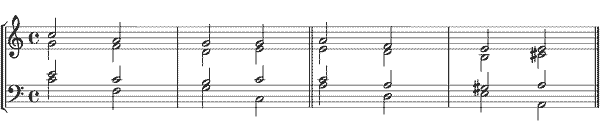
He colocado la implementación temperada (de temperamento igual) en primer lugar, a pesar de que históricamente es el último sistema en difundirse, porque es aquél al cual estamos más acostumbrados, y podemos usarlo como referencia comparativa (además de la justa entonación, el último sistema implementado en este archivo) para valorar los demás. En todos los casos, la referencia será la3 (A4) = 440 Hz. Para la comprensión general de los temperamentos, debemos pensar en el círculo de quintas, que se forma apilando quintas justas a partir de una nota cualquiera en una y otra dirección; cada quinta es reducida (temperada), y en algún caso agrandada, tal como se describe en el apartado correspondiente a cada sistema. Para más detalles, véanse las obras generales sobre sistemas entonativos citados en la Bibliografía. También puede verse una explicación general sobre los diversos sistemas en la página de esta web sobre Escalas y sistemas de entonación Sistema de temperamento igual(00'01'') El sistema de temperamento igual se caracteriza, como sabemos, por la división de la octava en doce intervalos de semitono iguales. Es decir, todas las quintas del círculo de quintas son reducidas en 1/12 de coma pitagórica. Por tanto, las notas enarmónicas (por ejemplo, re♯ y mi♭) tienen la misma altura, y todas las tonalidades son equivalentes, pudiéndose modular y transportar a cada una de ellas. Sin embargo, sabemos que en el sistema de temperamento igual todos los intervalos, excepto la octava, están desafinados. Las quintas son todas iguales, de 700 cents, muy próximas a las justas (701,96 cents). Sin embargo, las terceras mayores (400 cents) son apreciablemente más grandes que las justas (386,31 cents), y las terceras menores (300 cents), más pequeñas que las justas (315,64 cents). Por ello, se escuchan múltiples batimientos entre los armónicos de las notas que forman dichos intervalos y sus inversiones y ampliaciones. Sistema pitagórico(00'25'') El sistema pitagórico, con sus sensibles altas y sus semitonos cromáticos grandes y diatónicos pequeños (en sentido contrario a los de la justa entonación y los del sistema mesotónico), es equiparable a lo que se conoce como "entonación expresiva". En él, las quintas son justas (701,96 cents), pero las terceras mayores son incluso más grandes (407,82 cents) y armónicamente más desafinadas que las temperadas. Las terceras menores son más pequeñas (294,13 cents) y, por tanto, también más desafinadas que las temperadas. Ambos intervalos producen batimientos rápidos característicos. Recordemos que este sistema no es circular; es decir, si extendemos el "círculo de quintas" por ambos lados, obtenemos que dos notas enarmónicas no tienen la misma altura; por ejemplo, re♯ es más alta que mi♭. La diferencia entre ellas es la coma pitagórica, de fracción 531441/524288, equivalente a 23,46 cents). Por tanto, si se intenta aplicar directamente a un teclado de 12 notas por octava, sólo habrá una tecla para cada pareja de enarmónicas, que representará sólo una de las dos notas, pero no la otra; además existirá una quinta (en realidad, una sexta disminuida, de sol# a mi♭) completamente disonante, más pequeña que las demás, llamada quinta del lobo. La necesidad de repartir esta coma entre las diversas quintas originó la idea del temperamento. Temperamento mesotónico clásico(00'50'') El sistema de temperamento mesotónico clásico, o de 1/4 de coma, fue intoducido por Pietro Aron en 1523. Fue ampliamente usado en los instrumentos de teclado durante los siglos XIV y XVII. En realidad, este sistema surgió para intentar resolver el otro problema de la afinación pitagórica: el del carácter no puro de las terceras mayores pitagóricas, que resultan ser una coma sintónica (81/80 = 21,51 cents) más grandes que las justas. Se caracteriza por reducir (temperar) las quintas 1/4 de coma sintónica. Por tanto, el número característico de la quinta mesotónica es 1,5 dividido entre la raíz cuarta de 81/80, es decir, 1,495348781, equivalente a 696,58 cents. Como resultado, las terceras mayores más usadas son justas. Sin embargo, las terceras menores no lo son, y las quintas (esqueleto de los acordes y del sistema tonal) son fuertemente disonantes, mucho más que las del sistema temperado, y provocan batimientos muy desagradables en acordes largos y de sonoridad mantenida, como los del ejemplo. En cambio, en figuraciones rápidas, puesto que en la zona media del ámbito sonoro los batimientos producidos por las terceras suelen ser más rápidos que los de las quintas, estos batimientos de las quintas no tienen tiempo de producirse, y por ello se ha considerado este sistema, junto con otros sistemas históricos que también favorecen las terceras por encima de las quintas, como adecuados para la música instrumental renacentista y barroca. Además, este temperamento tampoco es cíclico. Al haberse reducido las quintas, ahora resulta que las notas enarmónicas difieren en un sentido contrario a las pitagóricas (ahora re♯ sería más grave que mi♭, como sucede también en la justa entonación, e igualmente el semitono diatónico es mayor que el cromático). Sin embargo, como sólo podemos usar 12 teclas, sólo una de las notas de cada pareja de enarmónicas estará representada; por ejemplo, en la disposición habitual, existen en el teclado fa♯, do♯, sol♯, mi♭ y si♭, pero no las enarmónicas correspondientes. La quinta del lobo, situada entre sol♯ y mi♭, resulta ser ahora más grande que la justa, y mucho más disonante que las otras. Por tanto, este sistema sólo puede ser practicado en unas pocas tonalidades, con muy pocas alteraciones. Sistema Werckmeister IV(01'15'') El sistema Werckmeister IV (1691) es uno de los llamados "buenos temperamentos" cíclicos irregulares barrocos. A diferencia de los mesotónicos, estos temperamentos son cíclicos, es decir, se cierran en sí mismos y no tienen quinta del lobo, puesto que la coma pitagórica se reparte entre todas las quintas. Por tanto, aunque con una distribución de distancias irregular, cada tecla puede representar al par de notas enarmónicas, y ello permite ejecutar en estos sistemas música en todas las tonalidades y modular a todas ellas. Sin embargo, y a diferencia del temperamento igual, el reparto de la coma pitagórica entre las diversas quintas es irregular, por lo que distintas quintas, y por tanto todos los demás intervalos y acordes, suenan diferentes unos de otros. Por ello, cada tonalidad está caracterizada por tener un "sabor" especial. El Werckmeister IV fue diseñado por su autor, Andreas Werckmeister, para ejecutar música en las tonalidades con pocas alteraciones. He elegido este sistema, en lugar del Werkmeister III, por esta razón, y además porque éste último da resultados parecidos a otros sistemas que veremos a continuación. El Werckmeister IV se caracteriza por reducir 1/3 de coma pitagórica algunas quintas del ciclo de quintas, concretamente las quintas si♭ · fa, do · sol, re · la, mi · si y fa♯ · do♯; además, las quintas sol♯ · re♯ y re♯ · la♯ (que comparte tecla con el si♭) son agrandadas en 1/3 de coma pitagórica. Por tanto, la reducción global es de una coma pitagórica, y el sistema se cierra. Las quintas fa · do, sol · re y la · mi son justas. Las quintas reducidas de Werckmeister IV tienen un número característico de 1,5 dividido entre la raíz cúbica de 531441/524288, es decir, 1,493239763, menor incluso que el de las quintas mesotónicas; por tanto, estas quintas (694,13 cents) son aún más disonantes que las mesotónicas, y por supuesto mucho más que las temperadas. Las dos quintas agrandadas también son muy malas, y ello contrasta con las tres quintas justas del sistema. Ninguna de las terceras es justa, pero las más usuales se acercan más a las justas que las del sistema temperado. Como resultado, se observa un enorme desequilibrio acústico entre los diferentes intervalos y acordes. Por ejemplo, el acorde de La m, con su quinta justa y su tercera menor próxima a las justas, se ve claramente favorecido. También mejoran, aunque en menor medida, los de Fa M, Sol M y La M, que son mejores que los temperados y los pitagóricos correspondientes, aunque, respecto a los mesotónicos, han perdido las terceras mayores puras. En cambio, los acordes de Do M, Mi M y Re m salen perjudicados por sus quintas muy desafinadas y sus terceras que se alejan de las puras. Este desequilibrio se acentuaría más en tonalidades con varios bemoles o varios sostenidos, por el carácter exageradamente grande de las terceras mayores la♭ · do y re♭ · fa y el enorme tono la♭ - si♭ (o sol♯ - la♯), de 219,44 cents, que atraviesa, en el círculo de quintas, las dos agrandadas. Sistema Kirnberger III(01'40'') El sistema Kirnberger III (1779) es otro de los "buenos temperamentos" cíclicos barrocos más conocidos, aunque apareció en plena época del clasicismo; su autor es Johann Philipp Kirnberger, un alumno de Johann Sebastian Bach. En el Kirnberger III, las quintas do · sol, sol · re, re · la y la · mi son reducidas 1/4 de coma sintónica, como en el mesotónico clásico. Para hacer cíclico el temperamento, es necesario reducir también otra quinta en una schisma (diferencia de la coma pitagórica menos la coma sintónica, de fracción 32805/32768, o 1,95 cents); resulta ser la quinta do♯ · fa♯ (o re♭ · sol♭). El resto de las quintas son justas. Como resultado, en el acorde de Fa M la quinta es justa, como en el sistema Werckmeister IV, y las terceras fa · la y la · do se acercan un poco más a las puras que en dicho sistema, sin llegar a serlo; por tanto, en el Kirnberger III este acorde resulta algo favorecido. En cuanto al acorde de Do M, resulta ser idéntico al del mesotónico clásico, con la quinta tan disonante como en éste (aunque algo menos que en el Werckmeister IV), y tiene la tercera mayor justa como el mesotónico. También el acorde de La m es idéntico al del mesotónico clásico, pero en este caso, es peor que el de Werkmeister IV, que tiene la quinta justa. El de Re m, con su quinta también pequeña, es un poco peor que el mesotónico, a causa de su tercera menor más alejada de la pura; sin embargo, es mejor que el de Werkmeister IV, pues tiene todos sus intervalos más próximos a los justos que éste. En cambio, los acordes de Sol M, Re M y La M son peores que los del mesotónico clásico, pues sus quintas son tan desafinadas como en éste, y sus terceras se van alejando cada vez más, por este orden, de las puras. El acorde de La M del Kirnberger III es ya claramente peor también que el temperado, pues todos sus intervalos están más alejados de los justos que éste. Los acordes de Mi M, Si M y Fa♯ M tienen la quinta justa, y sus terceras son ligeramente mejores que las pitagóricas porque en su formación recorren la quinta reducida en la schisma (do♯ · fa♯). Por el lado de las tonalidades con bemoles, los acordes tónicos mayores tienen todos sus quintas justas, y las terceras se van alejando de la pureza conforme vamos añadiendo bemoles, hasta llegar a La♭ M y Re♭ M, en que llegan a ser pitagóricas. En cuanto a las tonalidades menores, la evolución es similar. Por tanto, podemos decir que se trata también de un sistema muy desigual; en las tonalidades con pocos sostenidos las quintas son desafinadas pero las terceras son justas (la tercera do · mi, del acorde de Do M) o cercanas a las justas; ello favorece a estas tonalidades en las obras o pasajes de figuración rápida. En cambio, en las tonalidades con bemoles o con muchos sostenidos las quintas son justas, pero las terceras cada vez se alejan más de las justas hasta llegar a ser pitagóricas. Sistemas similares a éste, en cuanto al efecto sobre las distintas tonalidades, aunque quizá con una transición más suave, son el de Bach-Kellner (propuesto por H. A. Kellner en 1975 como pretendida reconstrucción del usado por Bach) y el de Vallotti, del s. XVIII. En el primero de ellos, se distribuye la coma pitagórica reduciendo en 1/5 de ésta cada una de las quintas do · sol, sol · re, re · la, la · mi y si · fa♯. En el segundo, se reducen en 1/6 de coma pitagórica las quintas do · sol, sol · re, re · la, la · mi, si y, según las versiones, fa · do o bien si · fa♯. Justa entonación(02'05'') En el sistema de la justa entonación, por definición, todos los intervalos consonantes son justos y los acordes mayores y menores son puros. Por tanto, no se escuchan batimientos. ConclusiónComo conclusión, podemos decir que ninguno de los temperamentos históricos supera en conjunto al de temperamento igual, puesto que, aunque en algunos de ellos ciertos intervalos o acordes se ven mejorados, otros empeoran respecto al sistema temperado actual. Podemos decir que el sistema de temperamento igual equilibra y reparte las disonancias de manera equitativa. Y, por suspuesto, ningún otro sistema puede compararse, en cuanto a pureza sonora testimoniada por la ausencia de batimientos, a la justa entonación. Las frecuencias (en Hz) de las notas utilizadas son las siguientes:
* En justa entonación, desdoblamos la nota re usando RE en el acorde de Sol M y RE– en el acorde de Re m. (Podéis ver aquí una descripción de la notación utilizada.) Los intervalos (en cents) de los acordes que aparecen, calculados para la triada en posición fundamental, a partir de frecuencias no redondeadas, son:
Amplitud de los armónicos utilizados para las notas sintetizadas en Audacity:
En mi obra La justa entonación: teoría y práctica, actualmente en preparación, se expone de manera detallada la teoría implícita en este archivo de sonido.
|
(Ver La justa entonación. Presentación)
Podéis entrar también en la página dedicada al proyecto en Facebook y hacer clic en "Me gusta" a fin de estar al día de todos los contenidos. Os presento también mi novela Un himno a la alegría (también disponible en catalán), uno de cuyos temas es, precisamente, la justa entonación. Disponible en la tienda Amazon. Us presento també la meva novel·la Un himne a l'alegria (també disponible en espanyol), un dels temes de la qual és, precisament, la justa entonació. Disponible en la tenda Amazon. |
| Presentación | Qué es la justa entonación | Teoría | Práctica | Sonidos | Obras musicales | Notación | Encuesta | Cómo colaborar |
| Inicio (Página de presentación) | Contacto | Arriba |


