Armónicos y consonancia

Sonidos. Intervalos

La altura o tono de un sonido musical, o nota, está determinado por la frecuencia de la onda periódica que forma dicho sonido. La frecuencia se mide en vibraciones por segundo, o hercios, cuyo símbolo es Hz.

Manteniendo todo lo demás constante, la frecuencia del sonido producido al vibrar una cuerda o el aire en un tubo es inversamente proporcional a la longitud de la cuerda o del tubo.

Recordemos que todo intervalo musical se expresa mediante un número real, que puede ser una fracción (y al cual también podremos llamar cociente indistintamente), que indica el cociente de las frecuencias de las notas que lo forman; es decir, indica la cantidad por la que se debe multiplicar la frecuencia de la primera nota —o de la inferior, si se trata de un intervalo armónico ascendente— para obtener la frecuencia de la segunda, o superior.

El número que corresponde a la octava es dos (o la fracción 2/1), pues la octava de una nota tiene una frecuencia doble de dicha nota.

Puede comprobarse fácilmente que el número (o fracción) que corresponde a una suma (superposición o concatenación) de intervalos es el producto de los números de los intervalos que lo forman. Inversamente, el número (o fracción) que corresponde a una resta de intervalos (a separar de un intervalo mayor otro menor) es el cociente de los números (o fracciones) de los intervalos que lo forman.

La magnitud de los intervalos también puede expresarse en cents, o centésimas de semitono temperado. Puede demostrarse que, para calcular en cents el valor de un intervalo cuyo número o cociente característico es n, debe aplicarse la fórmula x = 3986,3137 log₁₀ n.

La serie de los armónicos naturales

Cuando suena una nota musical, además del tono o frecuencia fundamental, que da nombre a la nota, suenan al mismo tiempo otros sonidos de frecuencias superiores que aparecen junto a dicha frecuencia fundamental y que reciben el nombre de armónicos o parciales.

Los sonidos armónicos pueden explicarse como si, al vibrar una cuerda de un instrumento o el aire en un tubo, no vibrase únicamente en su longitud completa, sino también por mitades, por tercios, por cuartas partes, y así sucesivamente, en un movimiento periódico complejo. La onda que representa este movimiento puede ser descompuesta en ondas elementales sinusoidales, que constituyen los armónicos, cuyas frecuencias son múltiplos de la frecuencia fundamental. De las intensidades relativas de los diferentes armónicos (que están relacionadas con la amplitud de las ondas elementales) depende el timbre de la voz o del instrumento en cuestión.

Por ejemplo, si consideramos la frecuencia fundamental de la nota do de 66 Hz como la del primer armónico, el segundo armónico será el que tiene frecuencia doble que la fundamental (132 Hz), y por tanto, será el do a la octava superior de la fundamental. El tercer armónico es de frecuencia triple que la fundamental (198 Hz) y corresponde a la nota sol; por tanto, forma respecto al segundo armónico un intervalo de fracción 3/2, que es la fracción característica de la quinta justa. El cuarto armónico tiene una frecuencia de 264 Hz, cuatro veces la fundamental y dos veces el segundo armónico; por tanto, será de nuevo la nota do, a una octava más alta que el segundo armónico. El quinto armónico tiene una frecuencia de cinco veces la fundamental (330 Hz), y corresponde a la nota mi; por tanto, el intervalo que forma con el do del cuarto armónico es una tercera mayor llamada justa o pura, de fracción 5/4. Y así sucesivamente.

Serie de los armónicos naturales a partir del do de 66 Hz. La cifra superior de cada nota indica el número de armónico, y la inferior, la frecuencia en hercios (Hz) o vibraciones por segundo. Las notas en negrita indican notaciones aproximadas para sonidos ajenos a nuestro sistema musical occidental, mientras que las notas con fondo blando pertenecen a la escala llamada natural o de Zarlino. La frecuencia fundamental se ha destacado mediante una nota más grande.

Concepto de consonancia

Cuando dos sonidos suenan juntos, el efecto físico de las vibraciones complejas de las ondas que producen, en forma de variaciones en la presión, se suma en el punto donde inciden, por ejemplo, en nuestro oído. Si las frecuencias fundamentales de los sonidos son tales que comparten entre sí numerosos armónicos, dichos armónicos entrarán en resonancia, se reforzarán unos a otros y producirán un efecto placentero al oído. Por tanto, un intervalo será más consonante cuantos más armónicos existan en común entre las notas que lo forman.

Resulta, pues, que el intervalo más consonante es la octava (por ejemplo, do·do), pues la nota más aguda y sus armónicos son todos armónicos de la nota más grave. Le sigue la quinta justa (por ejemplo. do·sol), pues los armónicos 2, 4, 8... de la nota superior coinciden con los armónicos 3, 6, 12... de la nota inferior; además, los armónicos 6, 12... del segundo sonido (nota re) se corresponden con los armónicos 9, 18... del primero, y los armónicos 10, 20... de sol (nota si) coinciden con los armónicos 15, 30... de do.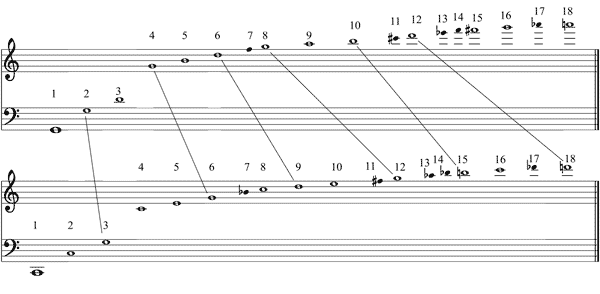

Armónicos coincidentes en el intervalo de quinta justa do·sol.

Igualmente son consonantes la cuarta justa (do·sol), inversión de la quinta justa; la tercera mayor pura (por ejemplo, do·mi), y su inversión, la sexta menor, y la tercera menor pura (do · mi ♭), y su inversión, la sexta mayor. Todos los demás intervalos son considerados disonantes, o al menos no son consonancias puras.

Por tanto, los intervalos consonantes son los que tienen como números o fracciones características 2 (octava), 3/2 (quinta justa), 4/3 (cuarta justa, inversión de la quinta justa), 5/4 (tercera mayor pura o justa), 6/5 (tercera menor pura), 5/3 (sexta mayor pura, inversión de la tercera menor pura) y 8/5 (sexta menor pura, inversión de la tercera mayor pura).

Batimientos o pulsaciones

En cambio, si las frecuencias fundamentales de dos notas, o bien las de algunos armónicos, están muy próximas una a otra pero no coinciden, los sonidos interferirán entre sí produciendo unas oscilaciones de intensidad características llamadas batimientos o pulsaciones (o batidos), de efecto desagradable al oído característico de la desafinación.

Todos estos temas, y otros relacionados, son expuestos detalladamente en mi obra La justa entonación: teoría y práctica, actualmente en preparación.

(Ver La justa entonación. Presentación)

¿QUÉ ES LA JUSTA ENTONACIÓN?

• ¿Qué significa afinar?
• Armónicos y consonancia
• Escalas y sistemas de entonación
• Sistema de temperamento igual
• El sistema de la justa entonación

Podéis entrar también en la página dedicada al proyecto en Facebook y hacer clic en "Me gusta" a fin de estar al día de todos los contenidos.

Os presento también mi novela Un himno a la alegría (también disponible en catalán), uno de cuyos temas es, precisamente, la justa entonación. Disponible en la tienda Amazon.

Us presento també la meva novel·la Un himne a l'alegria (també disponible en espanyol), un dels temes de la qual és, precisament, la justa entonació. Disponible en la tenda Amazon.